odeintを使った常微分方程式の数値計算 - とつとつとしてろうとせず

注意

以下の記述は私的な備忘録であり、内容の正確さに関しては一切保証いたしませんので、悪しからず。

概要

pythonの学習メモとしてscipyのodeintを使って常微分方程式を解いてみた。
実行環境はColaboratoryのjupyter notebookだす。

基本事項

odeintについて

"odeint"はscipyに含まれる常微分方程式を解く関数であり、ODEPACKのLSODAなるルーチンを使用しているとのこと。予測子修正子法であるAdams-Bashforth-Moulton法とBDF（後退差分法）を問題の硬さ（Stiffness）に応じて動的に切り替えているらしい。こんなのがコマンド一つで使えるなんて便利な世の中になったもんだなー。
なお、Runge-Kutta法（MATLABでいうところのode45）などの別の手法を使いたい場合は、odeintではなく"ode"という関数を使い、別途オプションで指定するそうだ（RK法なら"dopri5"オプション）。

実行例

まずは簡単な例として、単振り子の微分方程式を解いてみる。振り子の角度$\theta$に関する運動方程式は以下のようになる。
$\begin{align} \ddot{\theta} = - \frac{g}{l} \sin \theta \end{align}$
ここで、$g$は重力加速度、$l$は振り子の長さであり、上付きのドットは時間微分を表す。

常微分方程式（ODE）の数値計算について学んだ人にはおなじみの話だが、通常、ODEを解く場合は解きたい方程式を1階の微分方程式の連立方程式（ベクトル形）に書き換えてから入力してやる必要がある（いわゆる状態空間表現？）。

振り子の式を連立方程式に書き換えると、以下のようになる。
$\begin{align} \begin{aligned} \dot{x}_1 &= x_2 \\ \dot{x}_2 &= - \frac{g}{l} \sin x_1 \end{aligned} \end{align}$
ただし、状態変数として$\mathbf{x} = \left[ x_1 ,\ x_2 \right]^T = \left[ \theta ,\ \dot{\theta} \right]^T$とした。ベクトル形の表現になっている時点で左辺は常に同じ形（$\mathbf{\dot{x}}$）になるので、実際に入力として必要なのは右辺の項だけである。後はパラメータと初期条件（初期角度と初角速度）を設定してやれば結果が求められる。

まずは必要な関数をぞろぞろとインポートする。グラフを描くのにmatplotlibも必要なのはいつものこと。

import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from numpy import sin, sqrt
from scipy.integrate import odeint

後は時間（積分点）、パラメータ、初期条件、右辺の関数を定義してやり、odeintを実行するだけだ。「簡単でしょう？（CV：石井隆夫）」

g = 9.8 #重力加速度
l = 1.0 #振り子の長さ
q0 = 0.0 #初期角度
dq0 = 5.0 #初期角速度
x0 = [q0, dq0] #初期値ベクトル
t = np.arange(0,10,0.01) # 時間

# 振り子の運動方程式の右辺
def rhs1(x,t) :
  return [x[1], -g/l*sin(x[0])]

# 微小振幅として線形化した場合
def rhs2(x,t) :
  return [x[1], -g/l*x[0]]

# 数値積分の実行
x1 = odeint(rhs1, x0, t)
x2 = odeint(rhs2, x0, t)

ついでに微小振幅を仮定して線形化（$\sin \theta \approx \theta$）した場合の結果と比較してみる。
（そういえば$\theta$の代わりに$q$を使うのって誰が始めたんだろうな。大文字の形が似てるからだろうか？）

結果

適当に角度の時間変化をプロットしてやるとこうなる。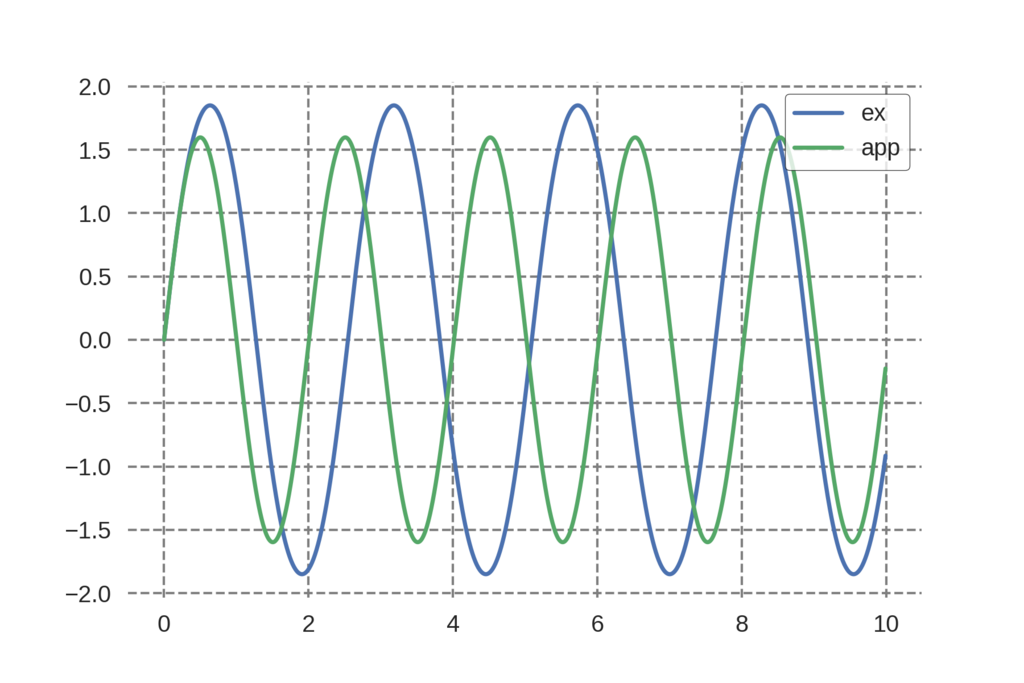

f:id:iqujack-lequina:20180429210212p:plain — 振り子の角度の時間変化

プロットの設定はこんな感じ。見た目を色々いじってるのは画像に保存するため。Colaboratoryのデフォルト設定だと見にくい気がしたもので。

%matplotlib inline
plt.xlabel('t')
plt.ylabel('x')
plt.axes(axisbg='white')
plt.grid(True, color='gray', linestyle='dashed')
plt.plot(t, x1[:,0], label='ex')
plt.plot(t, x2[:,0], label='app')
plt.legend(loc='upper right', frameon=True, facecolor='white', edgecolor='black')
plt.savefig('x-t.png', dpi=300, facecolor='white', transparent=False, format="png")

同じような感じで相平面図も描いてみた（横軸を位置、縦軸を速度に取ったプロット）。

f:id:iqujack-lequina:20180429210225p:plain — 振り子の相平面図

"ex"が元の式、"app"が線形化した式の結果だ。初期位置を0として初速を与えているが、初速がでかいのでオリジナルと微小振幅の結果はずれている（微小振幅の式は等時性が無理矢理にでも成り立っているが、オリジナルは破れている。振幅の大きさも当然異なる）。もちろん、振幅が小さくなるように初期条件を設定すれば両者はよく一致する。

なお、Colaboratoryのワークスペース上に保存したデータをダウンロードする場合は次のようにする。

import google.colab

google.colab.files.download('x-t.png')
google.colab.files.download('x-v.png')

Google Driveと連携するもっとスマートな方法もあるようだが、単純なデータのダウンロードならこれで十分だと思われ。

非線形振動

他のサンプルとして非線形振動のモデルとして有名なvan der Pol振動子とDuffing振動子もプロットしてみた。先程はパラメータを関数の引数に含めなかったが、odeintのオプションとして"args=(a,b,c)"みたいな形でパラメータも一緒に渡せる（ただし、パラメータが1つだけの場合もタプルで与える必要があるらしく、"args=(a,)"としてやらないとエラーになるっぽい）。
微分方程式はそれぞれ以下のようになる。

van der Pol方程式

$\begin{align} \begin{aligned} \dot{x}_1 &= x_2 \\ \dot{x}_2 &= \mu \left( 1 - x_1^2 \right) x_2 - x \end{aligned} \end{align}$

Duffing方程式

$\begin{align} \begin{aligned} \dot{x}_1 &= x_2 \\ \dot{x}_2 &= - k x_2 - x_1^3 + B \cos t \end{aligned} \end{align}$
特にDuffing方程式については適当なパラメータの下でジャパニーズ・アトラクタとして知られる図が見られるらしいのでやってみた。これは強制項の$\cos t$の周期に合わせて$2 \pi$ごとにプロットすることで得られるようだ。

x0 = [2.1, 0] #初期値ベクトル
t = np.arange(0,100,0.01) # 時間
ts = np.arange(0,2*np.pi*1000,2*np.pi) # ジャパニーズ・アトラクタのプロット用

# van der Pol振動子
mu = 3.0
def rhs3(x,t,mu) :
  return [ x[1], mu*(1-x[0]**2)*x[1]-x[0] ]

# Duffing振動子（ジャパニーズ・アトラクタ）
k = 0.05
B =7.0
def rhs4(x,t,k,B) :
  return [ x[1], -k*x[1]-x[0]**3+B*cos(t) ]

# 数値積分の実行
x3 = odeint(rhs3, x0, t, args=(mu,))
x4 = odeint(rhs4, x0, t, args=(k, B))
x5 = odeint(rhs4, x0, ts, args=(k, B)) # ジャパニーズ・アトラクタのプロット用